Rule In, Rule Out

As COVID-19 cases explode (at least in California), testing is more important than ever. There still are not enough tests, leading to supply-based restrictions in who can be tested and when. This is even before looking at the accuracy of the test itself. Contrary to some Facebook rumors, false negatives are a far greater concern than false positives. While a false positive might quarantine someone unnecessarily, a false negative can cause infected people to be thought of as “safe.” Anecdotally, there are a number of patients who have tested negative, sometimes several times, before the test finally correctly detects the infection. With the current data, what we have is a rule in test, not a rule out test, but since it’s the best we have, we need to use it to rule out infections.

With the current data, what we have is a rule in test, not a rule out test.

It has to do with something we call sensitivity and specificity. Sensitivity is how well a test is able to find the disease when the disease is present, while specificity is well the test picks up only that disease. A 100% sensitive test will find what it is looking for every time it is present. If it is there, the test will spot it. A 100% specific test will only find what it is looking for. If the test reports “found” it will always be that thing, not a lookalike. Generally the more sensitive, the more false positives; the more specific, the more false negatives.

Example: Sensitive Tests

Say we have a 100% sensitive 10% specific test. If we think of it like a metal detector, if there is any metal, the detector beeps. We dig and find…aluminum foil. There was metal, and our detector found it! With a test like this, when the detector doesn’t beep (negative), we can be confident that no metal is there. But we don’t know that when it does beep (positive), if we are going to dig up gold or trash.

Example: Specific Tests

Now say we have a 10% sensitive 100% specific test. We tune our metal detector to 79, the atomic number of gold. Now, when the detector beeps (positive), we dig and uncover pure gold. That may seem perfect, but, many gold things are actually alloys of gold plus some other metal: 10 karat or 14 karat gold isn’t worthless, even though it isn’t pure. In this configuration, we can be confident that we will always dig up gold, at the expense of missing other things that might or might not be neat.

Perfection

A theoretically perfect test would be 100% sensitive and 100% specific. When we ask our detector to find gold, it would give us pure gold as well as all the gold-containing alloys, but no nickel, no steel, no trash.

Wikipedia has a detailed article with illustrations for anyone interested in reading more about the math behind these numbers and other derived properties. However, as of July 2020 when I looked at it, it still had a warning banner common to many math-related Wikipedia pages:

This article may be too technical for most readers to understand.

Wikipedia banner

Folks who, unlike me, enjoy videos as a content delivery system may appreciate this twelve-minute production that Med Student Michaela would have watched in six minutes on 2x speed. Alternatively, I made a rudimentary sketch that Jason was kind enough to transform into a high-quality graphic.

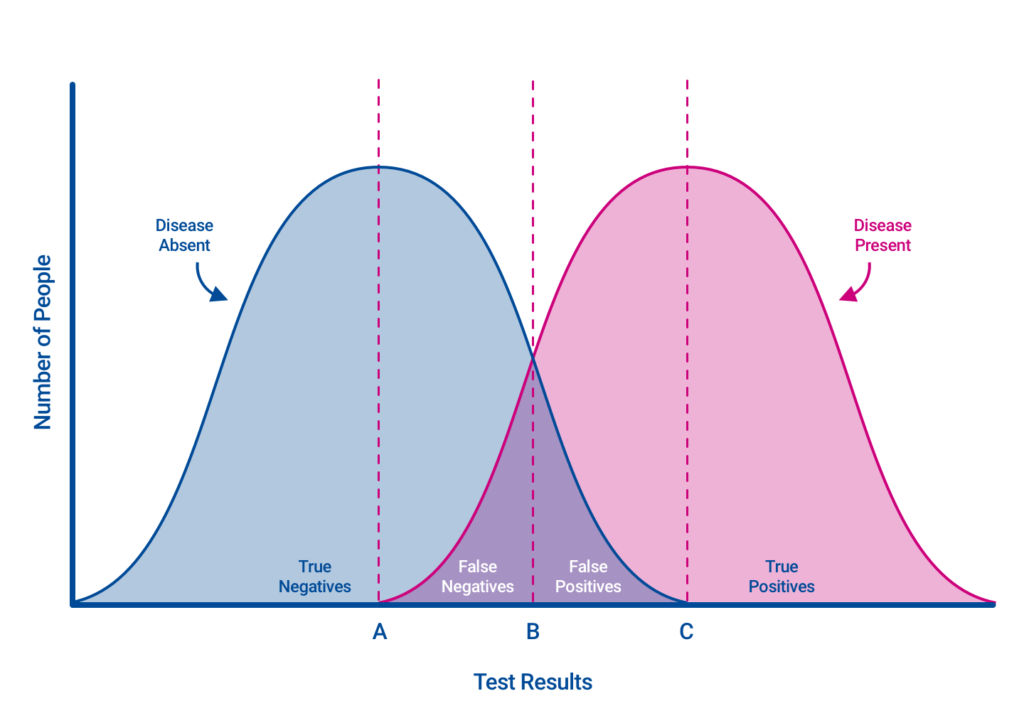
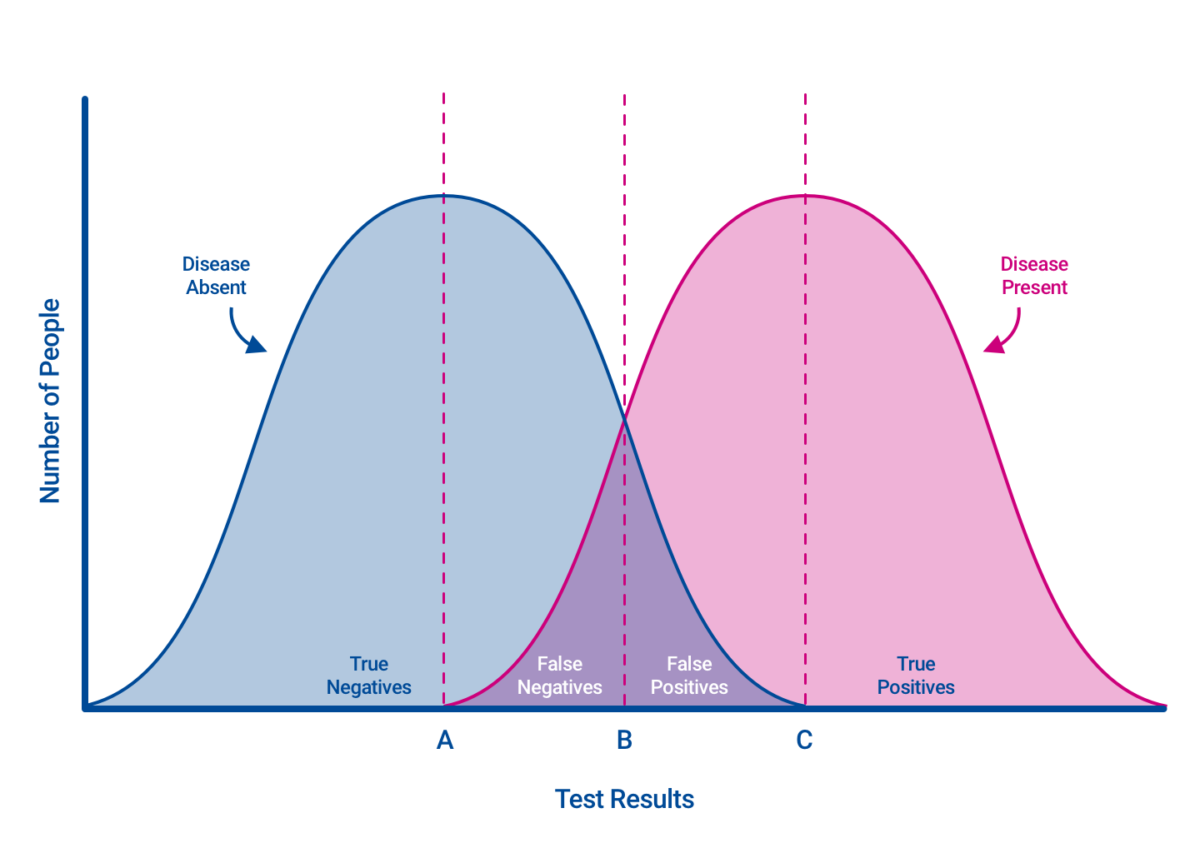
In this representation, the blue curve is negative results, while the pink curve is positive results. Bisexual Ambiguous results exist in the overlap between these curves. Say we’re building a test to find a Pride flag from a pile of assorted flags. Perhaps the most familiar Pride flag is the six-color rainbow, so we set the test cutoff to six (line B).

Rule: Six or more colors is a Pride flag.

With this rule, we’ll catch that flag as well as the original design with eight colors, the Philadelphia Pride flag with a different eight colors, and that Progress flag with its plentiful eleven colors.

Unfortunately, this cutoff also captures the flags of Dominica, South Africa, South Sudan, and the Olympics.

At the same time, there are other pride-type flags with fewer colors that we would miss, such as Bisexual, Non-Binary, Pansexual, and Transgender pride.

RULE: three OR MORE COLORS IS A PRIDE FLAG.

If we lowered the cutoff to three colors (line A), we’d capture all of these flags (no false negatives), but we would also collect hundreds of other false positive flags, like the United States and Colombia.

Rule: Seven colors is a pride flag.

If we raised the cutoff to seven colors (line C), we would eliminate the false positives, while losing all but the most variegated pride flags (many false negatives).

While the nomenclature and math may seem arcane, we use this kind of reasoning all the time in our everyday lives: when to stop microwave popcorn, how many guests to expect despite the RSVP numbers, or whether or not to wear a jacket when we leave the house in the early morning.

---

PCR (polymerase chain reaction) is Nobel Prize-winning microbiology technique: It takes a specific RNA sequence, or pattern, and only amplifies that sequence. If that pattern exists anywhere in the sample, it gets amplified. So why isn’t it a perfect test? Among other things, outside the microbiology lab, we are attempting to collect RNA, an unstable molecule, from a human being and preserve it long enough to get it to the PCR machine. We have to make sure we get a high-quality sample and put it directly into a medium that binds the RNA like glue so it doesn’t degrade.

Various sensitivity and specificity numbers exist for the COVID-19 tests, but for the sake of discussion, let’s pretend it has 70% sensitivity, ~100% specificity. A test like this, when positive, is definitely SARS-CoV2. Not influenza, not rhinovirus, not adenovirus, SARS-CoV2. Because it only finds that exact RNA pattern, half-chewed fragments might get missed…30% of the time.

We are attempting to collect RNA, an unstable molecule…and preserve it.

With 100% specificity, 10 positives = 10 positives. With 70% sensitivity, 10 negatives = 7 negatives and 3 false negatives. Thus we can rule the disease in; that is, we can say, “if the test is positive, we are sure they have it.” But we can’t really rule the disease out; instead we have to say, “Well, we can be 70% sure they don’t have it.”

In practical terms, the best way to stay safe is to assume everyone has it—spewing virus everywhere they go—and take appropriate precautions. This, dear reader, is why I need you to wear a mask.